快速幂相关 快速幂(二分幂) 时间复杂度:$O(logn)$
1 2 3 4 5 6 7 8 9 10 11 int Pow (int a,int b,int c) int res=1 ; while (b>0 ) { if (b&1 ) res=res*a%c; a=a*a%c; b>>=1 ; } return res; }
二分乘法 时间复杂度:$O(logn)$
用途 :用来解决乘法的结果远超long long范围,但需要的结果有取余的乘法运算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ll qmul (ll a,ll b,ll m) ll ans=0 ; ll k=a; ll f=1 ; if (k<0 ) {f=-1 ;k=-k;} if (b<0 ) {f*=-1 ;b=-b;} while (b){ if (b&1 ) ans=(ans+k)%m; k=(k+k)%m; b>>=1 ; } return ans*f; }
快速乘 和二分乘法用途一样,时间复杂度为$O(1)$
1 2 3 4 ll modmul (ll A,ll B,ll Mod) return (A*B-(ll)((long double )A*B/Mod)*Mod+Mod)%Mod; }
矩阵快速幂 其实矩阵快速幂的思想是和快速幂一样的,矩阵快速幂是用于快速求出一个矩阵的 n 次方的方法 。
首先,我们要知道,两个矩阵能不能相乘是有一定条件的:矩阵 A 的列数等于矩阵 B 的行数 ,那么这两个矩阵才可以进行相乘,否则这两个矩阵是不能相乘的。
矩阵乘法: 设$A=(a_{ij})$是一个$m\times s$的矩阵,$B=(b_{ij})$是一个$s\times n$的矩阵,那么规定矩阵A与矩阵B的乘积是一个$m\times n$的矩阵$C=(c_{ij})$,其中$C_{ij}=a_{i_1}b_{1_j}+a_{i_2}b_{2_j}+…+a_{i_s}b_{s_j}=\sum _{k=1}^{s}a_{i_k}b_{k_j}(i=1,2…m;j=1,2,…n)$
计算矩阵A(规模$n\times s$)与矩阵B(规模$s\times m$)相乘后得到$n\times m$的矩阵res
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> using namespace std ;int a[100 ][100 ],b[100 ][100 ];int res[100 ][100 ];void Matrix_mult (int n,int m,int s) for (int i=0 ;i<n;i++) for (int j=0 ;j<m;j++) for (int k=0 ;k<s;k++) res[i][j]+=a[i][k]*b[k][j]; } int main (int argc, char const *argv[]) int n,m,s; cin >>n>>m>>s; for (int i=0 ;i<n;i++) for (int j=0 ;j<s;j++) cin >>a[i][j]; for (int i=0 ;i<s;i++) for (int j=0 ;j<m;j++) cin >>b[i][j]; Matrix_mult(n,m,s); for (int i=0 ;i<n;i++) { for (int j=0 ;j<m;j++) cout <<res[i][j]<<"\t" ; cout <<endl ; } return 0 ; }
矩阵快速幂
时间复杂度: $O(logn)$
计算斐波那契的第N项,并对$1e9+7$取模
对于递推式$F[n]=F[n-1]+F[n-2]$,可构造矩阵:$\binom{F_{n+2}}{F_{n+1}}=\begin{pmatrix}
对于矩阵快速幂,最主要的是构造矩阵,矩阵构造出来了,答案也就出来了
ps:对于大多数用到矩阵快速幂的题目,也可以用BM算法来解决
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 #include <bits/stdc++.h> #define ll long long const int maxn=10 ;const int mod=1e9 +7 ;using namespace std ;struct mart { ll m[100 ][100 ]; }unit; mart mult (mart a,mart b) mart ans; int x; for (int i=0 ;i<4 ;i++) { for (int j=0 ;j<4 ;j++) { x=0 ; for (int k=0 ;k<4 ;k++) x=(x%mod+(a.m[i][k]%mod*b.m[k][j]%mod)%mod)%mod; ans.m[i][j]=x%mod; } } return ans; } void init () for (int i=0 ;i<4 ;i++) unit.m[i][i]=1 ; } mart qpow (mart a,ll b) init(); mart ans=unit; while (b) { if (b&1 ) ans=mult(ans,a); a=mult(a,a); b>>=1 ; } return ans; } ll slove (ll n) mart a,b; a.m[0 ][0 ]=1 ; a.m[0 ][1 ]=1 ; a.m[1 ][0 ]=1 ; a.m[1 ][1 ]=0 ; b.m[0 ][0 ]=1 ; b.m[1 ][0 ]=0 ; mart c=mult(qpow(a,n-2 ),b); return c.m[0 ][0 ]%mod; } int main (int argc, char const *argv[]) ll n; cin >>n; if (!n) cout <<0 <<endl ; else cout <<slove(n+1 )<<endl ; return 0 ; }
GCD、LCM、EXGCD、CRT相关 GCD 实现原理 :辗转相除法
时间复杂度:$O(log_2n)$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int gcd1 (int a,int b) return b?gcd1(b,a%b):a; } int gcd2 (int a,int b) int t; while (b) { t=a; a=b; b=t%b; } return a; }
LCM 公式:$LCM(a,b)=a*b/GCD(a,b)$
1 2 3 4 int lcm (int a,int b) return a/gcd*b; }
EXGCD 用途 :一般用来求解不定方程,求解线性同余方程,求解模的逆元等
如求解二元一次方程:$ax+by=c$,(a,b均为正整数,取最小正整数解)
存在x,y,使得$gcd(a,b)=ax+by$
注意:返回值为a和b的最大公约数,最后的x,y可以直接调用
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int exgcd (int a,int b,int &x,int &y) if (a==0 &&b==0 ) return -1 ; if (b==0 ) { x=1 ;y=0 ; return a; } int d=exgcd(b,a%b,y,x); y-=a/b*x; return d; }
例题 :设青蛙A的出发点坐标是x,青蛙B的出发点坐标是y。青蛙A一次能跳m米,青蛙B一次能跳n米,两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <bits/stdc++.h> #define LL long long #define INF 0x3f3f3f3f #define PI acos(-1.0) using namespace std ;LL exgcd (LL a,LL b,LL &x,LL &y) if (!b) { x=1 ; y=0 ; return a; } LL r=exgcd(b,a%b,x,y); LL t=y; y=x-(a/b)*y; x=t; return r; } int main () LL a,b,x,y,n,m,l,k1,k2; cin >>x>>y>>m>>n>>l; LL d=x-y; a=l; b=n-m; LL c=exgcd(a,b,k1,k2); if (d%c) printf ("Impossible" ); else { LL s=k2*d/c; LL v=a/c; printf ("%lld\n" ,(s%v+v)%v); } return 0 ; }
中国剩余定理(CRT) 问题: 今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
定理1:几个数相加,如果存在一个加数,不能被整数a整除,那么它们的和,就不能被整数a整除。
定理2:两数不能整除,若除数扩大(或缩小)了几倍,而被除数不变,则其商和余数也同时扩大(或缩小)相同的倍数(余数必小于除数)。
简单的说就是求$M\%A=a,M\%B=b,M\%C=c…$的M,其中A、B、C……互质
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #define ll long long int ex_gcd (ll a, ll b, ll &x, ll &y) ll d; if (b == 0 ) { x = 1 ; y = 0 ; return a; } d = ex_gcd(b, a % b, y, x); y -= a / b * x; return d; } ll chinese_remainder (ll b[], ll w[], ll len) ll i, d, x, y, m, n, ret; ret = 0 ; n = 1 ; for (i=0 ; i < len ;i++) n *= w[i]; for (i=0 ; i < len ;i++) { m = n / w[i]; d=ex_gcd(w[i], m, x, y); ret = (ret + y*m*b[i]) % n; } return (n + ret%n) % n; }
中国剩余定理扩展 求$M\%A=a,M\%B=b,M\%C=c…$的M,其中A、B、C……不互质
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 ll a[maxn],b[maxn]; ll ex_gcd (ll a,ll b,ll &x,ll &y) ll d; if (b==0 ) { x=1 ; y=0 ; return a; } d=ex_gcd(b,a%b,y,x); y-=a/b*x; return d; } ll ex_crt (ll *a, ll *b, int n) ll M=a[1 ],R=b[1 ],x,y; for (int i=2 ;i<=n;i++) { ll d=ex_gcd(M,a[i],x,y); if ((b[i]-R)%d) return -1 ; x=(b[i]-R)/d*x%(a[i]/d); R+=x*M; M=M/d*a[i]; R%=M; } return R>0 ?R:R+M; }
欧拉函数、元根相关 欧拉定理: 若$n,a$为正整数,且$n,a$互质,则:$a^{φ(n)}\equiv1(mod n)$;即:$a^{φ(n)}$与1在模$m$下同余。
欧拉定理实际上是费马小定理的推广
欧拉函数 对于正整数N,少于或等于N ([1,N]),且与N互质的正整数(包括1)的个数,记作$φ(n)$。(1-1/P1) (1-1/P2)… (1-1/Pn)$
直接求 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int Eular (int n) int eu=n; for (int i=2 ;i*i<=n;i++) { if (n%i==0 ) { eu-=eu/i; while (n%i==0 ) n/=i; } } if (n>1 ) eu-=eu/n; return eu; }
打表求
1 2 3 4 5 6 7 8 9 10 void Eular () euler[1 ]=1 ; for (int i=2 ;i<maxn;i++) euler[i]=i; for (int i=2 ;i<maxn;i++) if (euler[i]==i) for (int j=i;j<maxn;j+=i) euler[j]=euler[j]/i*(i-1 ); }
原根 定义: 对于两个正整数$(a,m)=1$,由欧拉定理可知:存在$d\leq m-1$。比如说欧拉函数$d=φ(m)$,即小于等于$m$的正整数与$m$互质的正整数的个数,使得$a^d\equiv1 (mod m)$。由此,在$(a,m)=1$时,定义$a$对模$m$的指数$\delta m(a)$为使$a^d\equiv1(mod m)$成立的最小正整数$d$。由前知$\delta m(a)$一定小于等于$φ(m)$,若$\delta m(a)=φ(m)$,则称$a$为$m$的原根
应用一: 求一个素数的最小的原根
m是正整数,a是正数,若$a\%m$的阶等于$φ(m)$,则a为模m的一个元根($φ(m)$表示m的欧拉函数)
给出一个素数p,找出p最小的元根
我的理解:找到最小的数x,使得 $x^{ϕ(n)}\%n=1$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 #include <bits/stdc++.h> const int maxn=1e6 +10 ;#define ll long long using namespace std ;int p[maxn];int k;ll Pow (ll a,ll b,ll c) ll res=1 ; while (b) { if (b&1 ) res=res*a%c; b>>=1 ; a=a*a%c; } return res; } void getp (ll n) for (int i=2 ;i*i<=n;i++) { if (n%i==0 ) { p[k++]=i; while (n%i==0 ) n/=i; } } if (n>1 ) p[k++]=n; } int main (int argc, char const *argv[]) ios::sync_with_stdio(false ); ll n; cin >>n; k=0 ; getp(n-1 ); for (int i=2 ;i<n;i++) { int flag=0 ; for (int j=0 ;j<k;j++) { if (Pow(i,(n-1 )/p[j],n)==1 ) { flag++; break ; } } if (!flag) { cout <<i<<endl ; return 0 ; } } return 0 ; }
应用二: 求原根的个数
定理: 如果$p$有原根,则它恰有$φ(φ(p))$个不同的原根,$p$为素数时,$φ(p)=p-1$,因此就有$φ(p-1)$个原根
对应题目:POJ1284
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std ;int Eular (int n) int eu=n; for (int i=2 ;i*i<=n;i++) { if (n%i==0 ) { eu-=eu/i; while (n%i==0 ) n/=i; } } if (n>1 ) eu-=eu/n; return eu; } int main (int argc, char const *argv[]) int p; while (cin >>p) { cout <<Eular(p-1 )<<endl ; } return 0 ; }
素数相关 埃拉托斯特尼篩法 时间复杂度:$O(nloglog(n))$, 空间复杂度$O(n)$
1 2 3 4 5 6 7 8 9 10 11 12 inline void init () memset (vis,0 ,sizeof (vis)); vis[0 ]=vis[1 ]=1 ; for (int i=2 ;i<maxn;i++) { if (!vis[i]) for (int j=2 ;j*i<maxn;j++) vis[j*i]=1 ; } }
欧拉筛法 线性筛法,拿空间换时间
时间复杂度:$O(n)$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 int vis[maxn];int prime[maxn];int cnt;inline void init () memset (vis,0 ,sizeof (vis)); memset (prime,0 ,sizeof (prime)); cnt=0 ; for (int i=2 ;i<maxn;i++) { if (!vis[i]) prime[cnt++]=i; for (int j=0 ;i*prime[j]<n;j++) { vis[i*prime[j]]=1 ; if (i%prime[j]==0 ) break ; } } }
筛素数+欧拉函数打表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 bool check[maxn+10 ];int phi[maxn+10 ];int prime[maxn+10 ];int tot; inline void phi_and_prime_table (int N) memset (check,false ,sizeof (check)); phi[1 ]=1 ; tot=0 ; for (int i=2 ;i<=N;i++) { if (!check[i]) { prime[tot++]=i; phi[i]=i-1 ; } for (int j=0 ;j<tot;j++) { if (i*prime[j]>N) break ; check[i*prime[j]]=true ; if (i%prime[j]==0 ) { phi[i*prime[j]]=phi[i]*prime[j]; break ; } else phi[i*prime[j]]=phi[i]*(prime[j]-1 ); } } }
唯一分解定理 定义:每个大于1的自然数,若不是本身就是质数,就是可写为2个以上的质数的积,而且这些质因子按大小排列之后,写法仅有一种方式
唯一分解定理具有:唯一性(分配方式的唯一性);存在性
例如:$6936=2^3\times3\times17^3$,$1200=2^4\times3\times5^2$
即:对于任一大于$1$的正整数$n$,都可以唯一分解成有限个质数的乘积:$n=p^{a_{1}}_{1}p^{a_{2}}_{2}\ldots p^{a}_{k}=\prod ^{k}_{i=1}p^{a_{i}}_{i}$(这里$p_i$为素数,其对应的指数$a_i$为正整数)
求质因子及其个数 描述: 给出一个数字n,求它的质因子及其个数,写成形如:n=p1^a1 + p2^a2…..的形式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 #include <bits/stdc++.h> using namespace std ;const int maxn = 1e6 +10 ;int a[maxn];int an[maxn];int num;void Prime_num (int n) memset (a,0 ,sizeof (a)); memset (an,0 ,sizeof (an)); num=0 ; for (int i=2 ;i*i<=n;i++) { if (n%i==0 ) { while (n%i==0 ) { a[num]=i; n/=i; an[num]++; } num++; } } if (n!=1 ) { a[num]=n; an[num++]++; } } int main () int n; while (scanf ("%d" ,&n)!=EOF) { Prime_num(n); printf ("%d的质因子的个数有%d个\n" ,n,num); printf ("%d=" ,n); for (int i=0 ;i<num-1 ;i++) printf ("%d^%d * " ,a[i],an[i]); printf ("%d^%d\n" ,a[num-1 ],an[num-1 ]); } return 0 ; }
约数个数定理 根据唯一分解定理:$n=\prod ^{k}_{i=1}p^{a_{i}}_{i}$,可知n的正约数个数为:$f\left( n\right) =\prod ^{k}_{i=1}\left( a_{i}+1\right)$
例如:求278000的约数个数
首先对278000进行质因数分解:$278000=2^4\times3^3\times5^3\times7^1$
然后可以计算出278000的约数个数共有$(4+1)\times(3+1)\times(1+1)=40$个
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <bits/stdc++.h> using namespace std ;const int maxn=1e6 +10 ;int prime[maxn],nprime; int vis[maxn]; void getprime () nprime = 0 ; memset (vis,0 ,sizeof (vis)); for (int i = 2 ; i <= maxn; i++) { int t = maxn/i; for (int j = 2 ; j <=t; j++) vis[i*j] = 1 ; } for (int i = 2 ; i <= maxn; i++) if (!vis[i]) prime[nprime++] = i; } int factor_count (int n) int ans = 1 ,sum; int k = sqrt (n*1.0 ); for (int i = 0 ; prime[i] < k; i++) { if (n % prime[i] == 0 ) { sum = 0 ; while (n % prime[i] == 0 ) { sum++; n /= prime[i]; } ans *= (sum+1 ); } } if (n > 1 ) ans *= 2 ; return ans; } int main (int argc, char const *argv[]) int n; cin >>n; getprime(); printf ("%d的约数一共有%d个\n" ,n,factor_count(n)); return 0 ; }
给出$x,y$,求$x^y$的因子个数对10007取模的结果
公式: $x^y=(p_1^{e_1}p_2^{e_2}…p_k^{e_k})^y=p_1^{ye_1}p_2^{ye_2}…p_k^{ye_k}$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> #define LL long long using namespace std ;const int MAX = 1e6 +10 ;const int INF = 0x3fffffff ;int a[MAX];int an[MAX];int num;void Prime_num (int n) memset (a,0 ,sizeof (a)); memset (an,0 ,sizeof (an)); num=0 ; for (int i=2 ;i*i<=n;i++) { if (n%i==0 ){ while (n%i==0 ) { a[num] = i; n/=i; an[num]++; } num++; } } if (n!=1 ) { a[num] = n; an[num++] ++; } } int main () int n,b; while (scanf ("%d%d" ,&n,&b)!=EOF) { Prime_num(n); printf ("%d的质因数个数有%d个\n" ,n,num); printf ("%d = " ,n); for (int i=0 ;i<num-1 ;i++) printf ("%d^%d * " ,a[i],an[i]); printf ("%d^%d\n" ,a[num-1 ],an[num-1 ]); for (int i=0 ;i<num;i++) an[i] *= b; LL ans =1 ; for (int i=0 ;i<num;i++) ans *= (an[i]+1 ); printf ("%d^%d的约数个数对10007取模后的结果为:%lld\n" ,n,b,ans); } return 0 ; }
约数和定理 对于一个大于1正整数n可以分解质因数:$n=p_1^{a_1}\times p_2^{a_2}\times p_3^{a_3}\times …\times p_k^{a_k}$,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 int prime[maxn],nprime;int vis[maxn];void getprime () nprime = 0 ; memset (vis,0 ,sizeof (vis)); for (int i = 2 ; i <= 450 ; i++){ int t = 450 /i; for (int j = 2 ; j <=t; j++) vis[i*j] = 1 ; } for (int i = 2 ; i <= 450 ; i++){ if (!vis[i]) prime[nprime++] = i; } } int pow_mod (int a,int n,int MOD) int ans = 1 ; while (n){ if (n&1 ) ans = (ans*a)%MOD; n >>= 1 ; a = (a*a)%MOD; } return ans; } int factor_sum (int n) int ans = 1 ,sum; int k = sqrt (n*1.0 ); for (int i = 0 ; prime[i] < k; i++){ if (n % prime[i] == 0 ){ sum = 0 ; while (n%prime[i] == 0 ){ sum++; n /= prime[i]; } ans *= (pow_mod(prime[i],sum+1 ,MOD)-1 )/(prime[i]-1 ); } } if (n > 1 ) ans *= ans(n*n-1 )/(n-1 ); return ans; }
组合数相关 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int C (int a,int b) int sum=1 ; for (int i=1 ;i<=b;i++) sum=sum*(a+1 -i)/i; return sum; } int A (int a,int b) int sum=1 ; for (int i=0 ;i<b;i++) sum=sum*(n-i); return sum; }
卢卡斯定理求组合数 表达式:$C_n^m\%mod=C_{n/p}^{m/p}\times C_{n\%mod}^{m\%mod}\%mod$
递推式:$(C_{n\%mod}^{m\%mod}\times Lucas(n/p,m/p))\%mod$(递归出口为$m==0$,$return 1$)
注意:mod必须为质数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <bits/stdc++.h> using namespace std ;typedef long long ll;const int maxn=1e5 +10 ;ll n,m,MOD; ll fac[maxn]; ll pow (ll a,ll b) ll r=1 ,base=a%MOD; while (b) { if (b&1 ) r=r*base%MOD; base=base*base%MOD; b>>=1 ; } return r%MOD; } void init () fac[0 ]=1 ; for (ll i=1 ;i<=maxn;i++) fac[i]=fac[i-1 ]*i%MOD; } ll C (ll n,ll m) if (n<m) return 0 ; return fac[n]*pow (fac[m]*fac[n-m],MOD-2 )%MOD; } ll Lucas (ll n,ll m) if (!m) return 1 ; else return Lucas(n/MOD,m/MOD)%MOD*C(n%MOD,m%MOD)%MOD; } int main (int argc, char const *argv[]) cin >>n>>m>>MOD; init(); cout <<Lucas(n,m)<<endl ; return 0 ; }
拓展卢卡斯定理 $1\leq m\leq n\leq1e18$,$2\leq mod\leq1e6$,不保证$mod$是素数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 #include <bits/stdc++.h> using namespace std ;typedef long long ll;ll p; const int MAXN=11 ;ll n,m; ll exgcd (ll a,ll b,ll &x,ll &y) if (!b) { x=1 ; y=0 ; return a; } ll res=exgcd(b,a%b,x,y),t; t=x;x=y;y=t-a/b*y; return res; } ll power (ll a,ll b,ll mod) ll sm; for (sm=1 ;b;b>>=1 ,a=a*a%mod) if (b&1 ) sm=sm*a%mod; return sm; } ll fac (ll n,ll pi,ll pk) if (!n) return 1 ; ll res=1 ; for (ll i=2 ;i<=pk;++i) if (i % pi) (res*=i)%=pk; res=power(res,n/pk,pk); for (ll i=2 ;i<=n%pk;++i) if (i%pi) (res*=i)%=pk; return res*fac(n/pi,pi,pk)%pk; } ll inv (ll n,ll mod) ll x,y; exgcd(n,mod,x,y); return (x+=mod)>mod?x-mod:x; } ll CRT (ll b, ll mod) return b*inv(p/mod,mod)%p*(p/mod)%p; } ll C (ll n,ll m,ll pi,ll pk) ll up=fac(n,pi,pk),d1=fac(m,pi,pk),d2=fac(n-m,pi,pk); ll k=0 ; for (ll i=n;i;i/=pi) k+=i/pi; for (ll i=m;i;i/=pi) k-=i/pi; for (ll i=n-m;i;i/=pi) k-=i/pi; return up*inv(d1,pk)%pk*inv(d2,pk)%pk*power(pi,k,pk)%pk; } ll exlucus (ll n,ll m) ll res=0 ,tmp=p,pk; int lim=sqrt (p)+5 ; for (int i=2 ;i<=lim;++i) if (tmp%i==0 ) { pk=1 ; while (tmp%i==0 ) pk*=i,tmp/=i; (res+=CRT(C(n,m,i,pk),pk))%=p; } if (tmp>1 ) (res+=CRT(C(n,m,tmp,tmp),tmp))%=p; return res; } int main () cin >>n>>m>>p; cout <<exlucus(n,m)<<endl ; return 0 ; }
容斥定理 描述: 要计算几个集合并集的大小,我们要先将所有单个集合 的大小计算出来,然后减去所有两个集合相交 的部分,再加回所有三个集合相交 的部分,再减去所有四个集合相交 的部分,依此类推,一直计算到所有集合相交 的部分。
公式:
公式的解释:目的是求解m个集合的并集,首先将m个集合相加,减去集合间两两相交的部分,加上三三相交的部分,再减去四四相交的部分……一直到m个集合相交的部分,当m为偶数时,最后一项的符号为负数,否则为正数。
应用一:
计算$1 \sim n$之间不能整除2,5,7的正整数有多少个
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <bits/stdc++.h> using namespace std ;int main (int argc, char const *argv[]) int n; cin >>n; int a=n/2 ; int b=n/5 ; int c=n/7 ; int d=n/(2 *5 ); int e=n/(2 *7 ); int f=n/(5 *7 ); int g=n/(2 *5 *7 ); int ans=n-(a+b+c-d-e-f+g); cout <<ans<<endl ; return 0 ; }
应用二:
计算$1 \sim n$之间不能整除a,b,c的正整数有多少个(应用一的升级版,对应NYOJ1160)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> #define ll long long using namespace std ;ll lcm (ll a,ll b) return a/__gcd(a,b)*b; } int main (int argc, char const *argv[]) ll n,a,b,c; while (cin >>n&&n) { cin >>a>>b>>c; ll _a=n/a; ll _b=n/b; ll _c=n/c; ll d=n/(lcm(a,b)); ll e=n/(lcm(a,c)); ll f=n/(lcm(b,c)); ll g=n/(lcm(a,lcm(b,c))); ll ans=n-(_a+_b+_c-d-e-f+g); cout <<ans<<endl ; } return 0 ; }
与二进制结合的容斥定理 二进制枚举的模板
1 2 3 4 5 6 7 8 int n; for (int i=0 ;i<(1 <<n);i++){ for (int j = 0 ; j < n ;j++) { printf ("%d " ,(i>>j)&1 ); } }
应用一: 求$[a,b]$区间与$n$互质的数的个数(对应题目:HDU4135)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <bits/stdc++.h> #define ll long long const int maxn=1e6 +10 ;using namespace std ;int A[maxn];ll lcm (ll a,ll b) return a/__gcd(a,b)*b; } int main (int argc, char const *argv[]) int t; ll a,b,n; scanf ("%d" ,&t); int x=0 ; while (t--) { ll ans1,ans; ans=ans1=0 ; map <int ,int >mmp; scanf ("%lld%lld%lld" ,&a,&b,&n); ll m=n; int k=0 ; for (int i=2 ;i*i<=m;i++) { if (m%i==0 ) { while (m%i==0 ) { if (mmp[i]==0 ) { A[k++]=i; mmp[i]=1 ; } m/=i; } } } if (m>1 ) { A[k++]=m; mmp[m]=1 ; } for (int i=1 ;i<(1 <<k);i++) { int cnt=0 ; ll tmp=1 ; for (int j=0 ;j<k;j++) { if (i>>j&1 ) { cnt++; tmp=lcm(tmp,A[j]); } } if (cnt&1 ) { ans+=(a-1 )/tmp; ans1+=(b)/tmp; } else { ans-=(a-1 )/tmp; ans1-=b/tmp; } } printf ("Case #%d: %lld\n" ,++x,(b-a+1 )-ans1+ans); } return 0 ; }
应用二: 求$[1,n]$中与$n$互质的数的平方和
平方和公式:$\sum ^{n}_{i=1}i^{2}=\dfrac {n\left( n+1\right) \left( 2n+1\right) }{6}$
把n进行质因子分解,进行容斥,结果=总和-不互质的平方和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 #include <cstdio> #include <algorithm> using namespace std ;typedef long long LL;const int maxn = 1e6 + 10 ;LL arr[maxn]; int p;LL get (LL x, LL y) LL cnt = x / y; return ((y * y) * (cnt * (cnt + 1 ) * (2 * cnt + 1 ) / 6 )); } void getp (LL n) p = 0 ; for (int i = 2 ; i * i <= n; i++) { if (n % i == 0 ) { arr[p++] = i; while (n % i == 0 ) n /= i; } } if (n > 1 ) arr[p++] = n; } int main () LL n; while (scanf ("%lld" , &n) != EOF) { if (n == 0 || n == 1 ) { puts ("0" ); continue ; } getp(n); LL sum = n * (n + 1 ) * (2 * n + 1 ) / 6 ; LL ans = 0 ; for (int i = 1 ; i < (1 << p); i++) { LL res = 0 , cnt = 1 ; for (int j = 0 ; j < p; j++) { if (i & (1 << j)) { cnt *= arr[j]; res++; } } if (res & 1 ) ans += get(n, cnt); else ans -= get(n, cnt); } printf ("%lld\n" , sum - ans); } return 0 ; }
鸽巢原理(抽屉原理) 描述:
若有$n$个笼子和$n+1$只鸽子,所有的鸽子都被关在鸽笼里,那么至少有一个笼子有至少$2$只鸽子。
若有$n$个笼子和$kn+1$只鸽子,所有的鸽子都被关在鸽笼里,那么至少有一个笼子有至少$k+1$只鸽子。
解题关键:弄清题目中,谁是鸽子谁是巢
例题 题1: 证明,如果从$\{1,2,3,….3n\}$中选择$n+1$个整数,那么总存在两个整数,他们之间的差最多为$2$。
解: 分组化简。将这$3n$个整数分组,$\{1,2,3\}$,$\{4,5,6\}$…..$\{3n-2,3n-1,3n\}$ 共$n$组。这样题目等价于:将$n+1$个整数放在$n$个盒子里。则根据原理,至少存在一个盒子里有两个数,这两个数之差最多为2。
题2: 证明,对于任意给定的52个整数,存在其中的两个整数,要么两者的和能被100整除。要么两者的差能被100整除。
解: 还是分组化简!将数这样进行分组:将所有整数的后两位尾数分组。$\{+0,-0,+100,-100,+200,-200….\}$,$\{+1,-1,+99,-99,+101,-101,+199,-199,+201,-201……\}$……$\{+49,-49,+51,-51,+149,-149,+151,……\}$$\{+50,-50,+150,-150,+250,-250……\}$ 这样。将所有的能被$100$整数的数分为$51$组(鸽子)。而从中取$52$个,(巢)。必有两个在同一组。得证。
题3: 一个学生有$37$天来准备考试,她知道她需要不超过$60$小时的学习时间,她还希望每天至少学习$1$小时。证明,无论如何安排学习时间(每天都是整数小时),都存在连续的若干天,在此期间她恰好学习了$13$个小时。
证明: 令$a_1$为她第一天学习的小时数,$a_2$为第二天的学习时数。这样。存在这样一个递增数列$a_1,a_2,a_3,……a_{37}$。满足:$1\leq a_1<a_2<a_3……a_{37}\leq 60$。同时,将这个数列每个数都加上13。则存在数列:$14\leq a1+13<a2+13<a3+13……a37+13\leq 73$。而这两个数列共有$37+37=74$个成员。这样。鸽子和巢终于出现^_^必然存在一个$a_i$,和一个$a_j$.使得$a_i=a_j+13$.就是说这两个数列中必然有两个差为$13$的数。得证。
题4: 一个袋子装了$100$个苹果,$100$个香蕉,$100$个橘子,$100$个梨子。如果我们每分钟从袋子里取出$1$种水果,那么需要多少时间我就能肯定至少已经拿出1打相同种类的水果。
解: 根据鸽巢原理加强形式:如果$q_1,q_2,,,,,q_n$为正整数,将$q_1+q_2+…..q_n-n+1$个物体放入$n$个盒子里。那么,至少存在一个盒子含有$q_n$个物体。对于此题:我们需要取$12$个水果。设已经取出了$11$个水果,还剩下一个。那么需要$11\times4+1$分钟。
题5: 证明对于任意$n+1$个整数$a_1,a_2,…..a_{n+1}$存在两个整数$a_i和a_j$,$i\neq j$,使得$a_i-a_j$能够被$n$整除。
解: 由于任一整数被n整除的余数有$0,1,2,……n-1$。 共$n$种,对于$n+1$个数,由鸽巢原理可得证。即存在$a_i,a_j$。$a_i=b_n+r,a_j=c_n+r (b>c)$。$a_i-a_j=(b-c)n$。所以$n|a_i-a_j$。至少两个整数被$n$整除的余数相等。
题6: 证明,边长为$2$的正方形中取$5$个点,当中存在$2$个点,这$2$点的距离至多为$\sqrt2$
解: 将正方形分成四等分即可。
Ramsey定理(拉姆齐二染色定理) 描述: 在$6$个人中,总有$3$个人互相认识或互相皆不认识
应用: 要找这样一个最小的数$R(k,l)=n$,使得$n$个人中必定有$k$个人相识或$l$个人互不相识
一些非平凡Ramsey数:
R(3, 3) = 6
卡特兰数 应用:
(1)一个栈(无穷大)的进栈序列为$1,2,3,…,n$,有多少个不同的出栈序列?
公式: $h\left( n\right) =\dfrac {C^{n}_{2n}}{n+1} \left(n= 1,2,3\ldots \right) $或$h\left( n\right) =C^{n}_{2n}-C^{n-1}_{2n} \left(n= 1,2,3\ldots \right) $
代码一:大数版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <stdio.h> #include <string.h> int a[105 ][1000 ];int b[105 ]; void catalan () int i, j, len, carry, temp; a[1 ][0 ] = b[1 ] = 1 ; len = 1 ; for (i = 2 ; i <= 100 ; i++) { for (j = 0 ; j < len; j++) a[i][j] = a[i-1 ][j]*(4 *(i-1 )+2 ); carry = 0 ; for (j = 0 ; j < len; j++) { temp = a[i][j] + carry; a[i][j] = temp % 10 ; carry = temp / 10 ; } while (carry) { a[i][len++] = carry % 10 ; carry /= 10 ; } carry = 0 ; for (j = len-1 ; j >= 0 ; j--) { temp = carry*10 + a[i][j]; a[i][j] = temp/(i+1 ); carry = temp%(i+1 ); } while (!a[i][len-1 ]) len --; b[i] = len; } } int main () catalan(); for (int i=1 ;i<=100 ;i++) { for (int j=b[i]-1 ;j>=0 ;j--) { printf ("%d" ,a[i][j]); } printf ("\n" ); } }
代码二:正常取模版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> #define ll long long #define ms(a) memset(a,0,sizeof(a)) const int N=1e4 +10 ;const ll Mod=19260817 ;using namespace std ;ll fat[N]; ll inv[N]; ll finv[N]; ll n; void Init () ll i; for (i=2 ,inv[1 ]=1 ;i<N;i++) inv[i]=((Mod - Mod/i)*1l l*inv[Mod%i])%Mod; for (i=1 ,fat[0 ]=1 ,finv[0 ]=1 ;i<N;i++) { fat[i]=(fat[i-1 ]*i)%Mod; finv[i]=(finv[i-1 ]*inv[i])%Mod; } } ll C (ll n,ll m) ll res=1 ; res=res*fat[n]%Mod; res=(res*finv[m]%Mod*finv[n-m]%Mod); return res; } ll Ctl (ll n) return (C(2 *n,n)-C(2 *n,n-1 )+Mod)%Mod; } int main (int argc, char const *argv[]) ios::sync_with_stdio(false ); Init(); while (cin >>n) cout <<Ctl(n)<<endl ; return 0 ; }
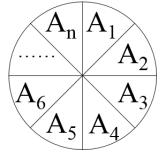
环涂色问题 题目描述:如下图,有$m(m\geq2)$个区域,如果给你$n(n\geq3)$种颜色,给这$m$个区域涂色,要求相邻的区域颜色不能一样,问一共有几种涂法
公式: $f(m)=(-1)^m\times (n-1)+(n-1)^m$
阶乘问题 大数阶乘 代码一:
计算$1e6$以内的数的阶乘即位数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <stdio.h> int main () int carry; int n,j; int a[40001 ]; int digit; int temp,i; while (scanf ("%d" ,&n)!=EOF) { a[0 ]=1 ;digit=1 ; for (i=2 ; i<=n; i++) { for (carry=0 ,j=1 ; j<=digit; ++j) { temp=a[j-1 ]*i+carry; a[j-1 ]=temp%10 ; carry=temp/10 ; } while (carry) { a[++digit-1 ]=carry%10 ; carry/=10 ; } } for (int k=digit; k>=1 ; --k) printf ("%d" ,a[k-1 ]); printf ("\n" ); printf ("length=%d\n" ,digit); } return 0 ; }
代码二:
计算$1e4$以内的数的阶乘
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> #define ll long long using namespace std ;const ll l=1e14 ;const int maxn=20000 ;ll f[maxn+1 ]; int main () ll n,c; ll d=1 ; scanf ("%lld" ,&n); memset (f,0 ,sizeof (f)); f[0 ]=1 ; for (int i=1 ;i<=n;i++) { c=0 ; for (int j=0 ;j<d;j++) { ll s=f[j]*i+c; f[j]=s%l; c=s/l; } if (c) f[d++]=c; } printf ("%lld" ,f[d-1 ]); for (int j=d-2 ;j>=0 ;j--) printf ("%014lld" ,f[j]); printf ("\n" ); return 0 ; }
斯特林公式 应用: 用来求$n!$的近似值
公式为:$\lim _{n\rightarrow \infty }\left( \dfrac {n}{\pi }\right) ^{n}\sqrt {\dfrac {2\pi n}{n!}}=1$,可以得出:$n!\approx \sqrt {2\pi n}\left( \dfrac {n}{e}\right) ^{n}$
计算$n!$的长度 公式: $len=\dfrac {\lg 2\pi n}{2}+n\lg \dfrac {n}{e}+1$($len$向下取整)
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 #include <bits/stdc++.h> using namespace std ;#define pi acos(-1.0) const double E=exp (1 );int main () int t; int n; cin >>n; long long ans=1 +0.5 *log10 (2 *pi*n)+n*log10 (n/E); cout <<ans<<endl ; return 0 ; }
阶乘最后非$0$位 复杂度:$O(nlogn)$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <stdio.h> #include <string.h> #define maxn 10000 int lastdigit (char buf[]) const int mod[20 ]={1 ,1 ,2 ,6 ,4 ,2 ,2 ,4 ,2 ,8 ,4 ,4 ,8 ,4 ,6 ,8 ,8 ,6 ,8 ,2 }; int len=strlen (buf),a[maxn],i,c,ret=1 ; if (len==1 ) return mod[buf[0 ]-'0' ]; for (i=0 ;i<len;i++) a[i]=buf[len-1 -i]-'0' ; for (;len;len-=!a[len-1 ]) { ret=ret*mod[a[1 ]%2 *10 +a[0 ]]%5 ; for (c=0 ,i=len-1 ;i>=0 ;i--) c=c*10 +a[i],a[i]=c/5 ,c%=5 ; } return ret+ret%2 *5 ; } int main () char n[maxn]; int a; while (scanf ("%s" ,n)!=EOF) { a=lastdigit(n); printf ("%d\n" ,a); } return 0 ; }
阶乘末尾$0$的个数 1 2 3 4 5 6 7 8 9 10 int find (int n) int count=0 ; while (n>0 ) { count+=n/5 ; n=n/5 ; } return count; }
计算逆元 逆元的定义: 对于正整数$a$和$m$,如果$ax\equiv 1(mod m)$,那么把这个同余方程中$x$的最小正整数叫做$a$模$m$的逆元
EXGCD计算逆元 1 2 3 4 5 6 7 8 9 10 11 int mod_reverse (int a,int m) int x,y; int d=exgcd(a,m,x,y); if (d==1 ) return (x%m+m)%m; else return -1 ; }
递归写法 注意:只能计算$a<m$的情况,并且要保证a和m互质
1 2 3 4 5 6 7 int inv (int a,int m) if (a==1 ) return 1 ; return inv(m%a,m)*(m-m/a)%m; }
利用欧拉函数求逆元 x和m互质(m可以使非素数);时间复杂度:$O({\sqrt{(n)}})$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 int eurler_phi (int n) int res = n; for (int i = 2 ; i * i <= n; i++) { if (n % i == 0 ) { res = res / i * (i - 1 ); while (n % i == 0 ) n /= i; } } if (n != 1 ) res = res / n * (n - 1 ); return res; } int inv (int a,int m) return Pow(a,eurler_phi(m)-1 ,m); }
快速幂求逆元 要求m为素数,a与m互质
公式: $inv=a^{m-1}\%m$
推导: $a^{m-1}\equiv1(mod m)\Rightarrow a\cdot a^{m-2}\equiv1(mod m)\Rightarrow a^{m-2}\equiv\dfrac {1}{a}(mod m)$
1 2 3 4 5 int inv (int a,int m) return Pow(a,m-2 ,m); }
线性时间求逆元 时间复杂度:$O(n)$
1 2 3 4 5 int inv[maxn];inv[1 ] = 1 ; for (int i=2 ;i<maxn;i++) inv[i]=(mod-mod/ i)*inv[mod%i]%mod;